Number of Continuous Subsequences With Sum S

• Problem Statement
• Naive Approach
• C++ Code
• Java Code
• Python Code
• Optimal Approach
• C++ Implementation
• Java Implementation
• Python Implementation
• FAQs

Problem Statement

Given an array a[], find the number of subarrays in it, which have a sum of k.

Subarray: A subarray of an array is formed by deleting some(possibly zero) elements from the beginning or end of the array.

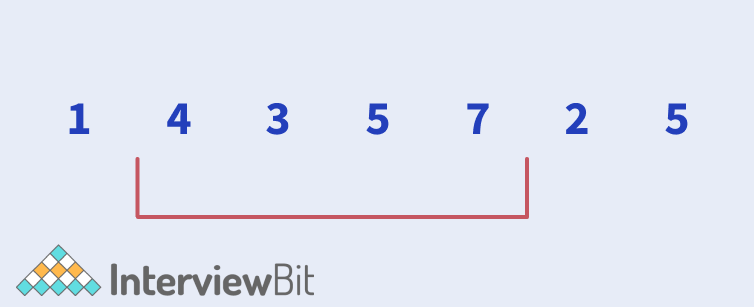
The red region shows a subarray of the original array.

Confused about your next job?

In 3 simple steps you can find your personalised career roadmap in Software development for FREE

Expand in New Tab

Sample Test Cases

Input 1: a = [10, 2, -2, -20, 10], k = -10
Output 1: 3
Explanation 1: The subarrays are listed as below (1 – Based Indexing):

• [4, 5]
• [1, 4]
• [2, 5]

Input 2: a = [1, 1, 1], k = 2
Output 2: 2
Explanation 2: All subarrays of length 2 are valid subarrays in this case, and there are a total of 2 such subarrays.

Naive Approach

The naive approach is to generate all the subarrays of the array and calculate their sum. Whenever we find a subarray with a sum equal to k, we increment our counter by 1. Finally, we return the count which keeps track of the number of subarrays with a sum equal to k.

Since there are a total of (n * (n + 1)) / 2 subarrays of an array, and each subarray will take O(n) time to traverse and calculate their sum, the required time complexity of this approach will be cubic in nature.

C++ Code

int countSubarraysWithSumK(vector < int > & a, int K) {   int n = a.size();   int count = 0;   for (int i = 0; i < n; i++) {     for (int j = i; j < n; j++) {       int sum = 0;       for (int k = i; k <= j; k++) {         sum += a[k];       }       count += (sum == K);     }   }   return count; }

Java Code

public static int countSubarraysWithSumK(int[] a, int K) {   int n = a.length;   int count = 0;   for (int i = 0; i < n; i++) {     for (int j = i; j < n; j++) {       int sum = 0;       for (int k = i; k <= j; k++) {         sum += a[k];       }       count += (sum == K ? 1 : 0);     }   }   return count; }

Python Code

def countSubarrayswithSumK(a, K):     n = len(a)     count = 0     for i in range(n):         for j in range(i, n):             sum = 0             for k in range(i, j + 1):                 sum += a[k]             count += sum == K     return count

Complexity Analysis

• Time Complexity: O(n³)
• Space Complexity: O(1)

Optimal Approach

We can solve this problem in linear time complexity using a hashmap-based approach. The algorithm is described as follows:

• Traverse the array, and keep track of the current running sum up to the ith index in a variable, say sum.
• Also, hash the different values of the sum obtained so far, into a hashmap.
• If the sum equals k  at any point in the array, increment the count of subarrays by 1.
• If this value of sum has exceeded k by a value of sum – k, we can find the number of subarrays, found so far with sum = sum – k, from our hashmap. Observe that if these subarrays are deleted from our current array, we will again obtain a sum of k. So, we add to our answer, the number of subarrays with sum = sum – k found so far from our hashmap.
• After traversing through the entire array once and applying the above steps, return the calculated result.

C++ Implementation

int countSubarraysWithSumK(vector < int > & a, int K) {   int n = a.size();   unordered_map < int, int > hash;   int count = 0, sum = 0;   for (int i = 0; i < n; i++) {     sum += a[i];     if (sum == K) {       count++;     }     if (hash.find(sum - K) != hash.end()) {       count += hash[sum - K];     }     hash[sum]++;   }   return count; }

Java Implementation

public static int countSubarraysWithSumK(int[] a, int K) {   int n = a.length;   HashMap < Integer, Integer > hash = new HashMap < > ();   int count = 0, sum = 0;   for (int i = 0; i < n; i++) {     sum += a[i];     if (sum == K) {       count++;     }     if (hash.get(sum - K) != null) {       count += hash.get(sum - K);     }     if (hash.get(sum) != null) {       hash.put(sum, hash.get(sum) + 1);     } else {       hash.put(sum, 1);     }   }   return count; }

Python Implementation

from collections import defaultdict   def countSubarrayswithSumK(a, K):     n = len(a)     hash = defaultdict(lambda: 0)     count = 0     sum = 0     for i in range(n):         sum += a[i]         if sum == K:             count += 1         if (sum - K) in hash:             count += hash[sum - K]         hash[sum] += 1     return count

Complexity Analysis

• Time Complexity: O(n)
• Space Complexity: O(1)

Practice Problem

Subarray With Given XOR

FAQs

Q. What is the time complexity of lookup in a hashmap?
A. The time complexity of lookup in a hashmap is O(1) amortized.

Q. Why is the number of subarrays of an array given by (n * (n + 1)) / 2?
A. The number of subarrays of an array can be calculated as there are,

• 1 subarray of length n
• 2 subarrays of length n – 1
• ……
• n subarrays of length 1

So, the total number of subarrays count out to a total of 1 + 2 + 3 + … n = (n * (n + 1)) / 2.

turnerprajectow.blogspot.com

Source: https://www.interviewbit.com/blog/subarray-sum-equals-k/

Share this post